Solution

The golden coin has a higher density than water. Is the coin situated on the pirates' ship, it pushes the ship a bit deeper into the water due to its gravitational force: the ship displaces more water. Archimedes found out, how much additional water the ship displaces with the gold coin on the ship. The principle, which was named after him, says:

The buoyant force of a body in a fluid equals the weight of the fluid displaced by the body.

Now: The weight of the water, which is additionaly displaced by the ship with the coin equals the weight of the coin. If we put the coin and the additionaly displaced water on scale, the scale would be in balance. But: The volume of the displaced water is much greater than the volume of the gold coin (see picture below).
This is due to the different densities: The density of gold is approximately 19times higher than the density of water. Although they have the same weight (and therefore the same mass), the volume of the water is therefore 19times higher than the volume of the gold coin.

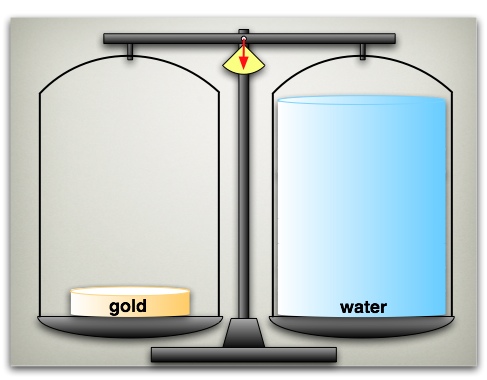
Solving the pirate's riddle, we have to take care about the two following points.

1. If we throw the coin overboard a ship into the sea the ship displaces less water:
   exactly the amount of water, which equals the weight of the coin. The volume of this amount of water equals the volume of the gold coin, which is approximately 19 times lower (right side of the scale, picture above). The sea level sinks.
2. The gold coin sinks into the sea. Now, exactly the amount of water is displaced, which equals the volume of the gold coin. The sea level rises.

Summary:
Because the coin sinks into the sea, the sea level rises again (see point two), but this rise is considerably smaller than the former sinking of the sea level (see point 1).
For this reason, the sea level will sink, if Schalckimnack throws a gold coin into the water.

By the way: How many coins Schalkimnack would have to throw into the sea so that no more water would be left?